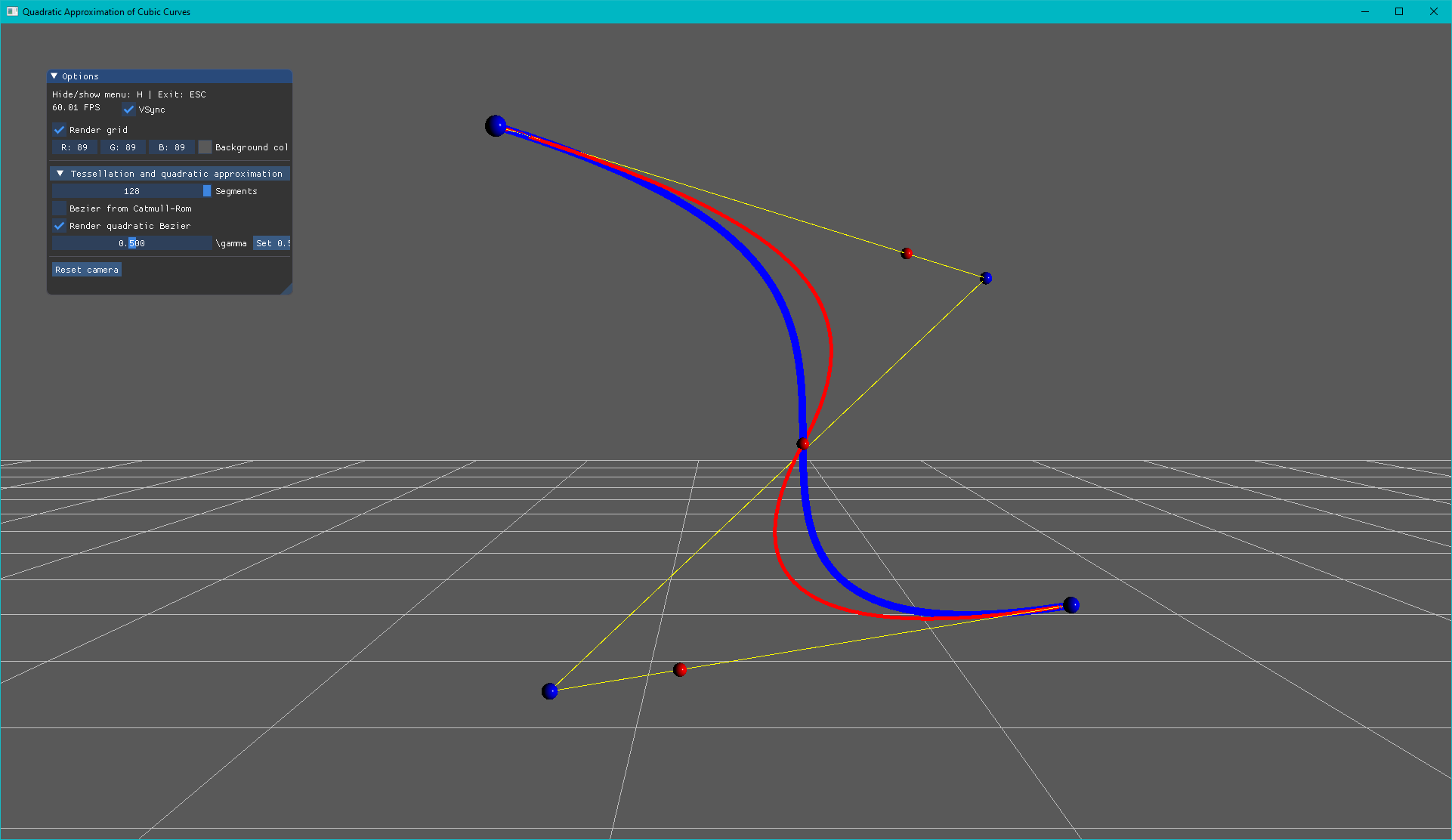
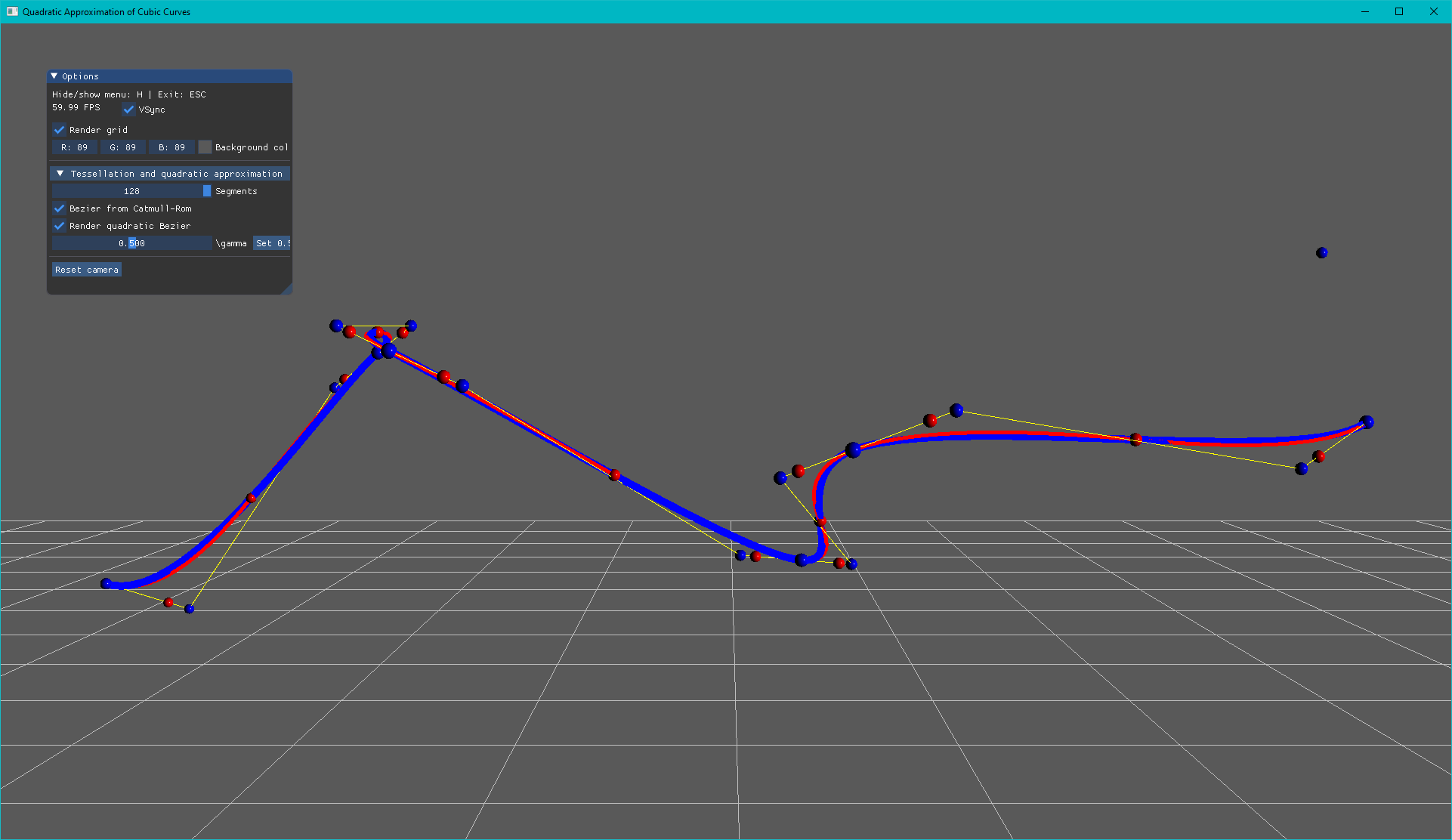
Quadratic Approximation of Cubic Curves

A simple degree reduction technique for converting piecewise cubic splines into piecewise quadratic splines that maintain parameterization and $C^1$ continuity.

Nghia Truong, Cem Yuksel and Larry Seiler
High-Performance Graphics 2020

Abstract

We present a simple degree reduction technique for piecewise cubic polynomial splines, converting them into piecewise quadratic splines that maintain the parameterization and $C^1$ continuity. Our method forms identical tangent directions at the interpolated data points of the piecewise cubic spline by replacing each cubic piece with a pair of quadratic pieces. The resulting representation can lead to substantial performance improvements for rendering geometrically complex spline models like hair and fiber-level cloth. Such models are typically represented using cubic splines that are $C^1$-continuous, a property that is preserved with our degree reduction. Therefore, our method can also be considered a new quadratic curve construction approach for high-performance rendering. We prove that it is possible to construct a pair of quadratic curves with $C^1$ continuity that passes through any desired point on the input cubic curve. Moreover, we prove that when the pair of quadratic pieces corresponding to a cubic piece have equal parametric lengths, they join exactly at the parametric center of the cubic piece, and the deviation in positions due to degree reduction is minimized.

Download

Paper: (preprint, 10MB pdf)
Code (github)
Windows binary

BibTeX

@article{Truong2020,
author = {Truong, Nghia and Yuksel, Cem and Seiler, Larry},
title = {Quadratic Approximation of Cubic Curves},
year = {2020},
issue_date = {August 2020},
publisher = {The Association for Computers in Mathematics and Science Teaching},
address = {USA},
volume = {3},
number = {2},
url = {https://doi.org/10.1145/3406178},
doi = {10.1145/3406178},
journal = {Proc. ACM Comput. Graph. Interact. Tech.},
month = aug,
articleno = {16},
numpages = {17}
}

WebGL Demo

Usage:
* Left mouse drag rotates the camera
* Right mouse drag translates the camera
* Mouse wheel zooms in/out
* S toggles smooth camera navigation

Notes:
* This WebGL demo requires WebAssembly-capable browser with WebGL enabled and may not work correctly in Firefox.
* The blue spheres are the control points of the cubic Bezier curve and red spheres are the control points of the approximated quadratic Bezier curves.
* The blue control points (spheres) can be move around. Just click on them, and some handles will show up that allow translation.

Initialization...